What are natural numbers?

We explain what natural numbers are and some of their characteristics. The greatest common factor and the least common multiple.

1. What are natural numbers?

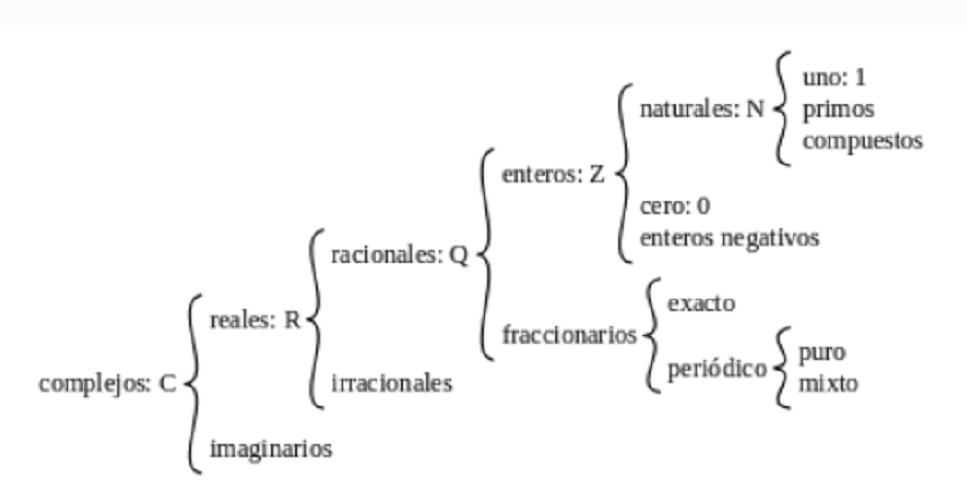
Natural numbers are the numbers that in the history of man first served to tell the objects , not only for accounting but also for ordering them. These numbers start from the number 1. There is no total or final amount of naturals numbers, they are infinite.

The naturals numbers are: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 … etc. As we see these numbers do not accept fractions (decimals). It should be clarified that the number zero is sometimes considered a natural number , but generally it is not.

On the other hand, it is said that naturals numbers always have a successor number. And natural numbers do not discriminate between numbers even and odd , the include them all. They do not accept fractions or negative numbers. They are distinguished from integers, since integers also comprise negative numbers. As for the written expression of naturals numbers, these are represented by the letter N, in uppercase.

Natural numbers are also the primary basis on which all mathematical operations and functions are based , addition, subtraction, multiplication and division. Also to trigonometric functions and equations. In short, they are the basic elements without which mathematics could not occur, also all the sciences that use this type of calculations such as geometry, engineering, chemistry , physics , all require mathematics and naturals numbers.

• The greatest common divisor. It is the largest natural number that has the mathematical ability to divide each of the given numbers. To find this number it is necessary, first to decompose the number into prime numbers, choose only common factors of lesser exponent and calculate the product of the factors.
• The least common multiple.  It is the smallest naturals number multiple of each of the numbers given in a particular distribution. And his steps to find it are the fact of breaking down the number into prime numbers, choosing prime factors of greater exponent and then calculating the product of those factors.

Mainly there are two uses that are fundamental, first  to describe the position of a given element within an ordered sequence , and to specify the size of a finite set, which in turn is generalized in the concept of cardinal number ( set theory). And secondly, the other use of great importance is that of the mathematical construction of whole numbers.

The order of natural numbers in a given operation does not alter the result , this is the so-called “commutative property” of naturals numbers.