What is analytical geometry?

We explain what analytical geometry is, its history, characteristics and most important formulas. In addition, its various applications.

1. What is analytical geometry?

Analytical geometry is a branch of mathematics dedicated to the in-depth study of geometric figures and their respective data, such as areas, distances, volumes , intersection points, angles of inclination, and so on. For this it uses basic techniques of mathematical analysis and algebra.

It uses a coordinate system known as the Cartesian Plane , which is two-dimensional and consists of two axes: one of abscissa (x axis) and another of ordinates (y axis). There you can study all the geometric figures that are of our interest, assigning to each point of the same a specific place of coordinates (x, y).

Thus, analytical geometry analyzes usually comprise the mathematical interpretation of a geometric figure , that is, the formulation of equations. Or it may be the opposite: the graphical representation of a mathematical equation. This equivalence is embodied in the formula y = f (x) , where f is a function of some kind.

Analytical geometry is a fundamental field of mathematics that is usually part of the high school curriculum.

2. History of analytical geometry

The founder of this field of study is considered the French philosopher René Descartes (1596-1650), with the appendix entitled ” La Geometrie ” in his famous work Discourse on the method .

However, in the eleventh century, the Persian mathematician Omar Khayyam (c.1048-c.1131) employed similar ideas, which Descartes could hardly know. In other words, both probably invented them on their own.

Given the hermetic ideas of Descartes, the Dutch mathematician Franz van Schooten (1615-1660) and his collaborators expanded, developed and disseminated analytical geometry in the West. It used to be called “Cartesian geometry”, to pay tribute to its creator, but that term today prefers to be used to refer only to the appendix written by Descartes.

3. Applications of analytical geometry

Analytical geometry is one of the most useful conceptual tools of humanity, and today its applications can be seen in, to name a few examples:

• The suspension bridges . From the old wooden suspension bridges, to its modern versions with steel cables, the geometric principle of the parabola is applied in each of them.
• The satellite dishes . The parabolic antennas to capture satellite information have the shape of a paraboloid, generated by its reflector that rotates on the axis, chasing the signal. Thanks to the reflection property of the parabola, the antenna disk can reflect the satellite signal to the power device.
• Astronomical observation . The celestial bodies orbiting on a path describing an ellipse, as deduced Johannes Kepler (1571-1630), not a circle, as he believed Copernicus (1473-1543). These calculations were possible only using analytical geometry.

4. Analytical Geometry Formulas

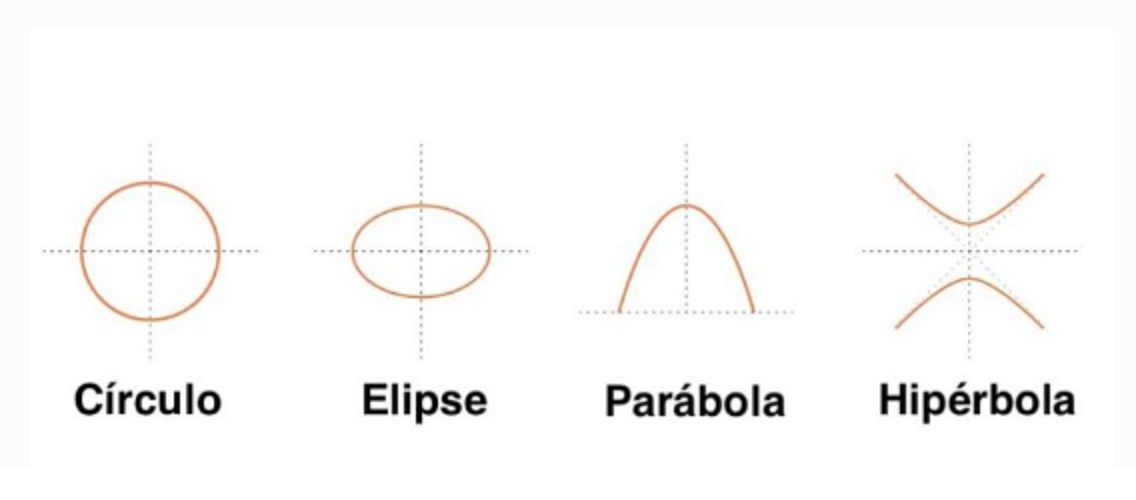
Geometry studies geometric figures and obtains their basic equations, such as:

• The lines are described by the formula ax + by = c .
• The circles are described by the formula x ² + y ² = 4 .
• The hyperbolas are described by the formula x = 1 .
• The parabolas are described by the formula y = ax ² + bx + c .
• The ellipses are described by the formula (x ² / a ² ) + (y ² / b ² ) = 1.