What Is Dynamics in Physics? Definition & Examples
dynamics, a branch of physical science and subdivision of mechanics is concerned with the motion of material objects in relation to the physical factors that affect them: force, mass, momentum, and energy.
Basic theoretical information
Basics of dynamics
If in kinematics only the movement of bodies is described, then in dynamics the causes of this movement under the action of forces acting on the body are studied.
Dynamics is a section of mechanics that studies the interaction of bodies, the causes of motion, and the type of motion that occurs. Interaction is a process in which the bodies interact with each other. In physics, all interactions are necessarily paired. This means that the bodies interact with each other in pairs. That is, any action necessarily generates a reaction.
Strength is a quantitative measure of the intensity of interaction between bodies. Force is the cause of a change in the speed of the body as a whole or its parts (deformation). Force is a vector quantity. The straight line along which the force is directed is called the line of action of the force. Strength is characterized by three parameters: the point of application, the module (numerical value) and the direction. In the International System of Units (SI), force is measured in Newtons (N). Calibrated springs are used to measure forces. Such calibrated springs are called dynamometers. Strength is measured by stretching a dynamometer.
The force exerting on the body is the same effect as all the forces acting on it, taken together, is called the resultant force . It is equal to the vector sum of all forces acting on the body:
To find the vector sum of several forces, you need to complete a drawing, where all the forces and their vector sum are drawn correctly, and according to this drawing, using knowledge from geometry (mainly the Pythagorean theorem and the cosine theorem), find the length of the resulting vector.
Types of forces:
1. Gravity. Attached to the center of mass of the body and directed vertically down (or the same thing: perpendicular to the horizon line), and is equal to:
where: g – acceleration of free fall, m – body mass. Do not confuse: gravity is perpendicular to the horizon, and not the surface on which the body lies. Thus, if the body lies on an inclined surface, the force of gravity will still be directed strictly downwards.
2. Friction force. Attached to the surface of contact of the body with the support and directed tangentially to it in the direction opposite to that which pulls, or other forces are trying to pull the body.
3. The force of viscous friction (force of resistance of the medium). It occurs when the body moves in a liquid or gas and is directed against the speed of movement.
4. Reaction force support. It acts on the body from the side of the support and is directed perpendicular to the support from it. When the body rests on an angle, then the reaction force of the support is directed perpendicular to the surface of the body.
5. Thread tension force. Directed along the filament from the body.
6. The strength of elasticity. It occurs during the deformation of the body and is directed against the deformation.
Pay attention and note for yourself the obvious fact: if the body is at rest, then the resultant of forces is zero.
Projection of forces
In most tasks on dynamics, more than one force acts on the body. In order to find the resultant of all forces in this case, you can use the following algorithm:
- Find the projections of all forces on the axis of the OX and sum them with their signs. So get the projection of the resultant force on the axis OX.
- Find the projections of all forces on the axis OY and sum them with their signs. So get the projection of the resultant force on the axis OY.
- The resultant of all forces will be found by the formula (Pythagorean theorem):

At the same time, pay special attention to the fact that:
- If the force is perpendicular to one of the axes, then the projection onto this axis will be equal to zero.
- If, when projecting a force on one of the axes, the sine of the angle “emerges”, then when projecting the same force on the other axis there will always be a cosine (of the same angle). When projecting on which axis the sine or cosine is easy to remember. If the angle is adjacent to the projection, then when the force is projected onto this axis, there will be a cosine.
- If the force is directed in the same direction as the axis, then its projection on this axis will be positive, and if the force is directed in the opposite direction to the axis, then its projection on this axis will be negative.
Newton’s Laws
The laws of dynamics, describing the influence of various interactions on the movement of bodies, were in one of their simplest forms, first formulated clearly and clearly by Isaac Newton in the book Mathematical Principles of Natural Philosophy (1687), therefore these laws are also called Newton’s Laws. The Newtonian formulation of the laws of motion is valid only in inertial reference systems (ISO) . ISO is a reference system associated with a body moving by inertia (uniformly and rectilinearly).
There are other restrictions on the applicability of Newton’s laws. For example, they give accurate results only as long as they are applied to bodies whose speeds are much less than the speed of light, and the size is much larger than the size of atoms and molecules (a generalization of classical mechanics to bodies moving at an arbitrary speed is relativistic mechanics, and to bodies whose dimensions are comparable to atomic ones – quantum mechanics).
Newton’s first law (or the law of inertia)
Formulation: In ISO, if no forces act on the body or the action of the forces is compensated (that is, the resultant of the forces is zero), then the body maintains a state of rest or uniform rectilinear motion.
The property of bodies to maintain their speed in the absence of action on it of other bodies is called inertia. Therefore, Newton’s first law is called the law of inertia. So, the reason for the change in the speed of movement of the whole body or its parts is always its interaction with other bodies. For a quantitative description of the change in body movement under the influence of other bodies, it is necessary to introduce a new quantity – body mass.
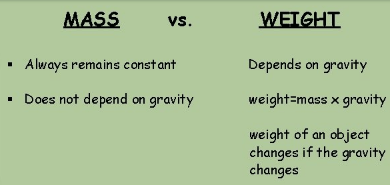
Mass is a property of the body, characterizing its inertness (ability to maintain speed constant. In the International System of Units (SI), body weight is measured in kilograms (kg). Body weight is a scalar quantity. Mass is also a measure of the amount of a substance:

Newton’s second law – the basic law of dynamics
Getting to the formulation of the second law, it should be remembered that in the dynamics two new physical quantities are introduced – body mass and force. The first of these quantities, mass, is a quantitative characteristic of the inert properties of the body. It shows how the body reacts to external influence. The second, force, is a quantitative measure of the action of one body upon another.
Formulation: Acceleration acquired by the body in ISO, directly proportional to the resultant of all forces acting on the body, and inversely proportional to the mass of this body:

However, when solving problems on dynamics, Newton’s second law should be written in the form:
If several forces simultaneously act on a body, then the force in the formula expressing Newton’s second law must be understood as the resultant of all forces. If the resultant force is equal to zero, then the body will remain in a state of rest or uniform rectilinear motion, since acceleration will be zero (Newton’s first law).
Newton’s Third Law
Formulation: In ISO, bodies act on each other with forces equal in magnitude and opposite in direction, lying on one straight line and having the same physical nature:

These forces are applied to different bodies and therefore cannot balance each other. Please note that you can only add forces that simultaneously act on one of the bodies. When two bodies interact, forces appear that are equal in magnitude and opposite in direction, but cannot be added, because they are attached to different bodies.
Algorithm for solving problems by dynamics
Problems in dynamics are solved using Newton’s laws. The following procedure is recommended:
1. Having analyzed the condition of the problem, determine which forces act and on which bodies;
2. Show in the figure all the forces in the form of vectors, that is, directional segments applied to the bodies on which they act;
3. Choose a reference system, while it is useful to direct one coordinate axis to the same direction as the acceleration of the body under consideration, and the other perpendicular to the acceleration;
4. Write the Newton’s II law in vector form:

5. Go to the scalar form of the equation, that is, write all its terms in the same order in the projections on each of the axes, without signs of the vectors, but considering that the forces directed against the selected axes will have negative projections, and thus in the left part of Newton’s law, they will be deducted, and not added. As a result, you get expressions like:
6. Create a system of equations, complementing the equations obtained in the previous paragraph, if necessary, with kinematic or other simple equations;
7. Further carry out all the necessary mathematical stages of the solution;
8. If several bodies participate in the movement, the analysis of forces and the writing of equations is carried out for each of them separately. If the task describes several situations according to dynamics, then a similar analysis is performed for each situation.
When solving problems, consider the following: the direction of the velocity of the body and the resultant forces do not necessarily coincide.
Elastic force
Deformation refers to any change in the shape or size of the body. Elastic is called such deformations in which the body fully restores its shape after the termination of the action of the deforming force. For example, after the load was removed from the spring, its length in the undeformed state did not change. During the elastic deformation of the body, a force arises that seeks to restore the former dimensions and shape of the body. It is called the force of elasticity. The simplest type of deformation is deformation of one-sided tension or compression.
With small deformations, the elastic force is proportional to the deformation of the body and is directed in the direction opposite to the direction of movement of the body particles during deformation:
where: k is the stiffness of the body, x is the amount of stretching (or compression, deformation of the body), it is equal to the difference between the final and initial length of the deformable body. And neither its initial nor final length is equal to each other. Stiffness does not depend on the magnitude of the applied force, nor on the deformation of the body, but is determined only by the material from which the body is made, its shape and size. In the SI system, stiffness is measured in N / m.
The statement about the proportionality of the force of elasticity and deformation is called Hooke’s law . The technique often used spiral springs. When the springs are stretched or compressed, elastic forces arise, which also obey the Hooke’s law. The coefficient k is called the spring stiffness. Within the limits of the applicability of Hooke’s law, the springs are capable of greatly changing their length. Therefore, they are often used to measure forces. A spring, the extension of which is calibrated in units of force, is called a dynamometer.
Thus, each particular body (and not a material) has its own rigidity and it does not change for a given body. Thus, if you have several times stretched the same spring in the dynamic problem, you should understand that its rigidity was the same in all cases. On the other hand, if the task had several springs of different dimensions, but, for example, they were all steel, then nevertheless they all will have different stiffnesses. Since stiffness is not a characteristic of a material, it cannot be found in any tables. The rigidity of each particular body will be either given to you in the problem of dynamics, or its value should be the subject of some additional research in solving this problem.
During compression, the force of elasticity prevents compression, and during tension – prevents tension. Consider also how you can express the rigidity of several springs connected in a certain way. With parallel connection of the springs, the overall stiffness coefficient is calculated by the formula:

When the springs are connected in series, the overall stiffness coefficient can be found from the expression:

Body weight
The force of gravity with which the bodies are attracted to the Earth must be distinguished from the weight of the body. The concept of weight is widely used in everyday life in the wrong sense, by weight is meant mass, but this is not so.
Body weight is the force with which the body acts on a support or suspension. Weight – force, which, like all the forces measured in Newtons (and not in kilograms), and is denoted by P . It is assumed that the body is motionless relative to the support or suspension. According to the third law of Newton, the weight is often equal to either the force of the support reaction (if the body lies on the support), or the tension force of the thread or the elastic force of the spring (if the body hangs on the thread or spring). Immediately make a reservation – the weight is not always equal to the force of gravity .
Weightlessness is a condition that occurs when the weight of the body is zero. In this state, the body does not act on the support, but on the support of the body.
The increase in body weight caused by the accelerated movement of the support or suspension is called overload . Overload is calculated by the formula:
where: P is the weight of the body experiencing an overload, P 0 is the weight of the same body at rest. Overloading is a dimensionless quantity. This is clearly seen from the formula. Therefore, do not believe science fiction writers who measure it in their books in g .
Remember that the weight is never shown in the figures. It is simply calculated by the formulas. And the figures depict the tension force of the thread or the reaction force of the support, which according to the third law of Newton is numerically equal to the weight, but directed in the other direction.
So, we note once again three essential points in which are often confused:
- Despite the fact that the weight and reaction force of the support are equal in magnitude and opposite in direction, their sum is not equal to zero. These forces can not be folded at all, because they are attached to different bodies.
- Do not confuse weight and weight. Mass is the body’s own characteristic, measured in kilograms, weight is the force of action on a support or suspension, measured in Newtons.
- If it is necessary to find the body weight P , then first find the reaction force of the support N , or the tension force of the thread T , and according to Newton’s third law the weight is equal to one of these forces and is opposite in direction.
Friction force
Friction is a type of interaction between bodies. It arises in the area of contact between two bodies during their relative movement or an attempt to cause such a movement. Friction, like all other types of interaction, obeys Newton’s third law: if a friction force acts on one of the bodies, then the force of the same magnitude, but in the opposite direction, acts on the second body.
Dry friction that occurs when bodies are relatively at rest is called resting friction. The force of static friction is always equal in magnitude to the external defiant force and directed in the opposite direction. The force of static friction can not exceed some maximum value, which is determined by the formula:

where: μ is a dimensionless quantity, called the coefficient of static friction, and N is the support reaction force.
If the external force is greater than the maximum value of the friction force, a relative slip occurs. The friction force in this case is called the sliding friction force . It is always directed in the direction opposite to the direction of movement. The force of sliding friction can be considered equal to the maximum force of static friction.
The coefficient of proportionality μ is also called the coefficient of sliding friction. The coefficient of friction μ is a dimensionless value. The friction coefficient is positive and less than one. It depends on the materials of the contacting bodies and on the quality of the processing of their surfaces. Thus, the coefficient of friction is a certain specific number for each specific pair of interacting bodies. You cannot find it in any tables. For you, it must either be given in the problem, or you yourself must find it in the course of the solution from any formulas.
If, as part of the solution of the problem, you get a friction coefficient greater than one or a negative one – you incorrectly solve this problem in dynamics.
If in the condition of the problem they are asked to find the minimum force under the action of which the movement begins, then they are looking for the maximum force under the action of which the movement does not start yet. This allows us to equate the acceleration of bodies to zero, and thus significantly simplify the solution of the problem. In this case, the friction force is considered equal to its maximum value. Thus, the moment at which an increase in the desired force by a very small amount immediately causes movement is considered.
Features of solving problems in multi-body dynamics
Related bodies
Algorithm for solving problems of dynamics in which several bodies are connected by threads:
- Make a drawing.
- Write the second law of Newton for each body separately.
- If the thread is not stretchable (and so it will be in most tasks), then the accelerations of all the bodies will be the same in modulus.
- If the thread is weightless, the block has no mass, there is no friction in the axis of the block, then the tension force is the same at any point of the thread.
Body movement through the body
In problems of this type it is important to take into account that the friction force on the surface of the contacting bodies acts on the upper body and the lower body, that is, friction forces arise in pairs. At the same time, they are directed in different directions and have an equal size, determined by the weight of the upper body. If the lower body is also moving, then it must be borne in mind that it is also affected by the frictional force from the side of the support.
Rotational movement
When a body moves in a circle, no matter in which plane the movement occurs, the body will move with a centripetal acceleration, which will be directed to the center of the circle along which the body moves. At the same time, the concept of a circle should not be taken literally. A body can pass only an arc of a circle (for example, move along a bridge). In all tasks of this type, one of the axes is necessarily chosen in the direction of the centripetal acceleration, i.e. to the center of the circle (or circular arc). The second axis should be directed perpendicular to the first. The rest of the algorithm for solving these problems coincides with the solution of other problems in terms of dynamics:
1. Having chosen the axes, write down Newton’s law in projections on each axis, for each of the bodies participating in the task, or for each of the situations described in the task.
2. If necessary, supplement the system of equations with the necessary equations from other topics in physics. Especially well need to remember the formula for centripetal acceleration:

3. Solve the resulting system of equations by mathematical methods.
There are also a number of tasks for rotation in a vertical plane on a rod or thread. At first glance it may seem that such tasks will be the same. This is not true. The fact is that the rod may experience deformations of both tension and compression. The thread is impossible to squeeze, it immediately bends, and the body on it simply falls through.
Movement on the thread. Since the thread will only stretch, then when the body moves on the thread in a vertical plane, only tensile deformation will occur in the thread and, as a result, the elastic force arising in the thread will always be directed to the center of the circle.
Body movement on the rod. The core, unlike the thread, can shrink. Therefore, at the highest point of the trajectory, the speed of the body attached to the rod may be equal to zero, in contrast to the thread, where the speed must be not less than a certain value so that the thread does not fold. The elastic forces arising in the rod can be directed both to the center of the circle, and in the opposite direction.
Turn the car. If the body moves along a solid horizontal surface in a circle (for example, a car passes a turn), then the force that holds the body along the path will be the friction force. In this case, the force of friction is directed in the direction of rotation, and not against it (the most common mistake), it helps the car to turn. For example, when the car turns to the right, the friction force is directed in the direction of the turn (to the right).
The law of the world. Satellites
All bodies are attracted to each other with forces that are directly proportional to their masses and inversely proportional to the square of the distance between them. Thus, the law of the world in the form of a formula is as follows:

Such a record of the law of universal perception is valid for material points, balls, spheres, for which r is measured between centers. The coefficient of proportionality G is the same for all bodies in nature. It is called the gravitational constant . In the SI system, it is equal to:
One of the manifestations of the force of world wideness is gravity. It is so called to call the force of attraction of bodies to the Earth or another planet. If M is the mass of the planet, R p is its radius, then the acceleration of free fall at the surface of the planet :

If you move away from the Earth’s surface at some distance h , then the acceleration of free fall at this height becomes equal (using simple transformations, you can also get the ratio between the acceleration of free fall on the planet’s surface and the acceleration of free fall at some height above the planet’s surface):
We now consider the question of artificial satellites of the planets. Artificial satellites move outside the atmosphere (if there is one on the planet), and only the forces of the planet act on them. Depending on the initial velocity, the trajectory of the cosmic body may be different. We consider here only the case of movement of an artificial satellite in a circular orbit almost at zero height above the planet. The radius of the orbit of such satellites (the distance between the center of the planet and the point where the satellite is located) can be approximately taken to be equal to the radius of the planet R p . Then the centripetal acceleration of the satellite, imparted by the forces of companion, is approximately equal to the acceleration due to gravity g. The speed of a satellite in an orbit near the surface (at zero height above the surface of the planet) is called the first cosmic velocity . The first cosmic velocity is found by the formula:
The movement of the satellite can be considered as a free fall, similar to the movement of shells or ballistic missiles. The only difference is that the satellite’s speed is so great that the radius of curvature of its trajectory is equal to the radius of the planet. For satellites moving along circular trajectories at a considerable distance from the planet, gravitational attraction weakens inversely proportional to the square of the radius r of the trajectory. The satellite speed in this case is found using the formula:
Kepler’s law for the periods of revolution of two bodies revolving around one attracting center:
If we are talking about the planet Earth, it is easy to calculate that with a radius r of the orbit equal to approximately 6.6 R З , the orbital period of the satellite will be equal to 24 hours. A satellite with such a period of revolution, launched in the plane of the equator, will still hang over a point on the earth’s surface. Such satellites are used in space radio communication systems. An orbit with a radius of r = 6.6 R 3 is called geostationary .